It’s about time I got my astronomy blog going again so I thought I’d start by explaining what I’ve been up to over the past two years or so in an area of study on the possible existence of exoplanets around a certain type of binary star system known as Post Common Envelope Binary (PCEB) systems.
I got into this area of research after meeting fellow Selsey astronomer John Mallett in 2019. John is part of a small group of amateur astronomers who have been researching in this area for a few years and I was recruited into their number almost straight away. The group goes by the name of ALTAIR Eclipsing Binary Research Group and here is a link to the about page of our website which is written and maintained by myself. The site is private to the four of us who are currently members, but the about page is publicly accessible. You can access all the published papers from the ALTAIR group on the About page – I have only been involved in the most recent one, but I am very busy writing parts of a new paper which is in progress.
The technique used to determine if an unseen third body (an exoplanet or perhaps a brown dwarf) might be orbiting one, or both of the stars in the PCEB system is called the method of Eclipse Time Variation (ETV). The rest of this article explains this in more detail.
Let’s clear up some terminology…
Exoplanets
Exoplanets are planets that orbit stars other than the Sun. It is an amazing fact that we had no evidence of the existence of any exoplanets until 1992, although it was widely assumed that the Sun could not be unique in having a family of planets (and other smaller bodies) in orbit around it. Such are the vast distances between the stars, it is only in these past few decades that the technology has existed to detect the existence of exoplanets, and it is only very recently that any exoplanets have been directly observed – most are detected by more subtle, indirect means – more about this shortly as it is pertinent to this story. To put it into perspective, there are now well over 4000 ‘confirmed’ exoplanets, and the number has been doubling every 27 months. However, only 16 exoplanets have been discovered using the ETV method that we, the Altair Group, are studying.
See NASA’s exoplanet website for lots of great information.
Post Common Envelope Binaries (PCEBs)
Binary stars are extremely common in the universe. A binary star system consists of two stars in a common orbit around each other. Star systems with three or more stars also exist. The specific type of binary systems that we are interested in are known as PCEB systems and evolve in a particular way, which I will briefly describe.
It is likely, in a binary system, that one of the stars will be more massive than the other. The more massive the star, the faster it ‘burns’ through the various stages of stellar fusion, and the faster it evolves. In this way, the more massive ‘primary’ star in the pair more quickly evolves into its red giant phase and expands enormously. (Our Sun will become a red giant in about 5 billion years). The primary star expands to the point where matter in its outer layers starts to overflow and transfers to the smaller secondary star. Thus, a common envelope of material is formed between the two stars. The secondary, typically a main-sequence star at this point (like our Sun), cannot cope with all this material that is being donated to it by the primary partner and, eventually, the common envelope is ejected from the star system altogether. The key here is that the departing envelope material takes angular momentum away with it, and the law of the conservation of angular momentum dictates that the two stars must be left with less angular momentum. This they achieve by moving closer together, which also causes their orbital period to decrease to the point where they spin around their common centre of gravity in a stunning, but typical time of two or three hours! During this process, the primary star will evolve on and will become either a white or red dwarf, whilst the secondary star stays as a main sequence star for a long period due to the fact that it started life as a fairly low mass star.
Eclipses
First, I should mention that it is generally not possible for us to make out the two separate stars using a telescope from here on Earth – certainly not with an amateur telescope, and this means we just see a single resulting point of light. So where does the eclipsing bit come in?
If the stars are aligned, even roughly, to our line of sight such that during their orbital dance, the stars move in front of each other, we will notice the following effects:
- When the stars are side by side, the combined point of light that we see will be at its brightest
- When the fainter of the stars moves in front of the brighter, we will see a larger dip in brightness (the primary eclipse)
- When the brighter of the stars moves in front of the fainter, we will see a smaller dip in brightness (the secondary eclipse)
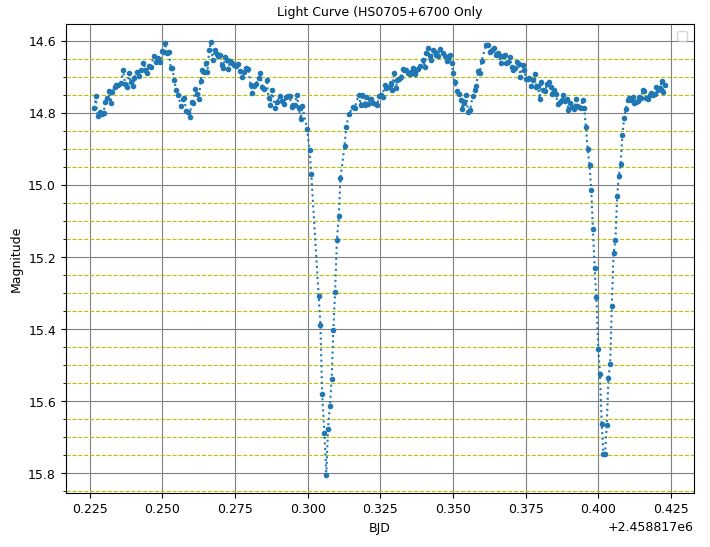
These effects are clearly illustrated in the graph of brightness (magnitude) over time shown below. We call this a light curve. I made these measurements at my observatory here in Ham of brightness (a process called photometry) of a star called HS0705+6700 (aka V0470 Camelopardalis) over a 4.5 hour period. The big dips are the primary ‘minima’ and the small ones are the secondaries. The binary orbital period of this star system is about 2.3 hours. The strange time scale at the bottom is in Julian Days with a correction for differences in the Earth’s position with respect to the barycentre of the Solar System. See here for more details about BJD, but know that this is the standard way astronomers in this field represent the date and time of the measurements. You can see on the graph that the primary dips are separated by just under 0.1 of a day which is where the 2.3 hours comes from.
Rotating Like Clockwork?
We might expect that the resulting whirling pair of stars will eclipse each other repeatedly and accurately, like celestial clockwork, and this would be true if we just considered the Keplerian equations of celestial mechanics. It would mean that, if we can measure the time of the minima with sufficient accuracy, we can work out the binary period and therefore we should be able to predict the time of any eclipse into the future (or back into the distant past).
This does actually hold accurately to a certain degree. We do indeed predict when eclipses should occur so that we can observe and measure them over the months and years after we have established the exact date and time of the first observed eclipse, and we are able to do this because, although the period is not exactly following Keplerian clockwork, it does so to a very high degree of accuracy – easily enough to pin down the time so that we can go out on the predicted night and be sure of capturing the minimum dip so that we can re-measure and refine the date and time once more.
However, in the real world there are several other known physical effects that can very slightly change the orbital period of the two stars. I will go into this shortly, but first let me introduce the tool we use to highlight any differences that might be seen in the binary period over time. The graph is called the O – C (pronounced “O minus C”) which stands for the Observed minus Calculated (or Computed) graph. An example taken from within our ALTAIR website for our friend HS0705+6700 is shown below:
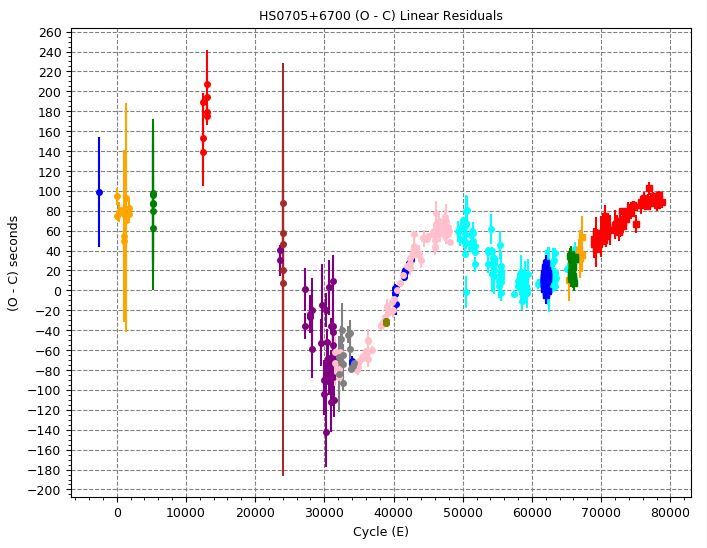
What we see in the O – C chart above is the Cycle or Epoch number of the eclipse plotted on the horizontal x-axis. The number of seconds difference from the expected calculated date and time of each minimum point is plotted on the y-axis. The different colours illustrate that the measurements were made by different groups of observers and research teams over the years (the legend is not shown here for clarity). The red group to the right has been made members of our ALTAIR group in the past few years (we try to observe this star every month if we can). As mentioned above, the period of HS0705+6700 is about 2.3 hours, so 80000 orbital cycles represent roughly 21 years of measurements. The zero Epoch is normally defined and agreed to be a certain historical observation and sometimes a measurement prior to this is found in the literature as is the case with the blue measurement with a negative cycle number at far left. The error bars tend to become smaller as time goes on due to improvements in technology. Some of the measurements on the left will have been made from photographic plates and photomultiplier detectors, whilst CCD cameras will have been used in more recent years.
Making sense of the O – C curve
The simplest way to compute the time of any epoch is to measure the period to the best accuracy possible and then add integer multiples of it to the date and time of the first epoch. If we call the Epoch number E, we can write a formula like this:
JDE = JD0 + E x Period
This is called the linear ephemeris. JD means Julian Date which is just a way of representing a date and time as a number. As I type this, the Julian Date is 2459444.8958333335. There are many on-line Julian Date converters available to try. They are handy because you can find differences between dates by subtracting them and calculate future dates by adding days to them. This is why it is common practice to quote the period of binary stars in days. For example, the period of HS0705+6700 is 0.09564668 days and the linear ephemeris for this star system is as follows:
JDE = 2451822.75964598 + E x 0.09564668
The value of the reference Julian Date of the JD0 in the above equation is a date back in October 2000. With this, you can now calculate the date and time of any epoch in the future, or past. If everything was purely working to Keplerian celestial mechanics, every point in the above O – C plot would be on the zero line and each point would be exactly 0.09564668 days apart, so we now must address why this is not the case.
Mechanisms that can Change the Binary Period
There are three mechanisms that are known to have an effect on the period of this kind of PCEB system and these are:
- The Applegate Effect
- Angular momentum loss
- The presence of a third, unseen body (or more than one unseen body).
Before I briefly explain these effects, I think you will be able to imagine that if we can calculate the sizes the first two effects, and we still find that they cannot account for the full magnitude of the O – C variations seen, then we are left with the conclusion that some unseen body must be the cause. This is the reasoning used so far by researchers in this field, and it is the way that those 16 ETV exoplanets mentioned above have been ‘discovered’.
Another thing that makes the above argument more convincing is that, when all other known effects have been subtracted from the O – C plots, what is often left over is a cyclic variation. Surely an exoplanet would leave a cyclic, periodic fingerprint behind as it goes around in its orbit?
Just a few words about the first two effects in the list above:
The Applegate Effect
A mechanism to potentially explain the eclipse time variations seen in O – C diagrams was proposed by Applegate in 1992. This process relies on the secondary star being magnetically active, undergoing solar-like magnetic cycles which are strong enough to redistribute the angular momentum (AM) within the star. No loss of AM from the system is required. This leads to shape changes which affect the gravitational quadrupole moment. Since the orbits of the stars are gravitationally coupled to variations in their shape, this effect could explain the small changes that are observed in the orbital period. We can calculate the magnitude of the AM variations seen in the O – C plots and then compute the size of the Applegate effect. Generally, it is found that the Applegate effect is at least an order of magnitude too small to explain the O – C variations (at least this is the case with the PCEBs that we are currently studying).
Angular Momentum Loss
Note that we are talking about a loss of AM, not a cyclic variation in AM. This means that there should be a gradual decrease in the period over time as the AM is lost. There are two causes of AM loss.
The first is caused by Gravitational Radiation. This is a consequence of Einstein’s General Theory of Relativity. Accelerated masses cause ripples in the geometry of space and time and carry energy away from the binary system.
The second effect is known a Magnetic Braking which is a theory explaining the loss of stellar AM due to material getting captured by the stellar magnetic field and thrown out to a great distance from the surface of the star.
The sizes of both of these effects can be calculated. Often, like the Applegate effect, their contributions are not enough to explain the O – C variations seen.
Once this work has been done and the known effects have been subtracted, the remaining job is to calculate the number, mass and orbits of potential exoplanets that could explain the cyclic variations in the O – C. As you can imagine, this is not an easy task!
Our current work focuses on following up with lots of new eclipse timings for the 18 stars in our canon. We are interested in how the proposed exoplanets are faring against our new timings.
Further Discussions
This blog article is an overview of our work. I have not explained any details about how we observe and measure the brightness of the stars, nor how we analyse the light curves to calculate the times of minima. We have written several Python tools to do all this and maybe the next blog will go into a bit more detail.